Срочно! даны уравнения одной из сторон ромба x-3y+10=0 и одной из его диагоналей x+4y-4 =...

Question

Дан 1 ответ

Правильный ответ

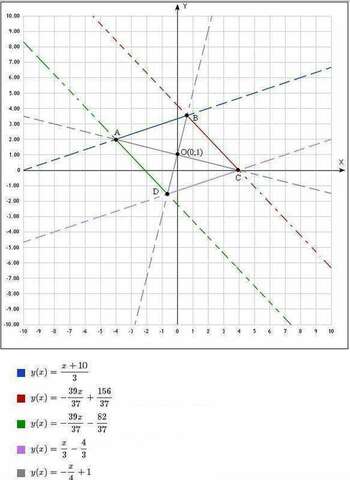
Уравнение стороны $AB=\frac{10+x}{3}$

1) Т.к. диагонали в ромбе взаимно перпендикулярны, то должно выполняться равенство:
пусть $y_{1}= \frac{4-x}{4}=-\frac{1}{4}x+1$ - уравнение диагонали АС
а $y_{2}=kx+b$ - уравнение диагонали BD
тогда: $-\frac{1}{4}*k=-1$ => $k=4$
Т.к. точка О - точка пересечения диагоналей ромба, то: b=1
y=4x+1 - уравнение диагонали BD

2) Координаты точки А(-4;2):
A∈AB, A∈AC
AB∧AC=A
$\frac{4-x}{4}=\frac{10+x}{3}$
x=-4, y=2.

3) Координаты точки С(4;0):
т.О - середина АС, тогда:
т. $O( \frac{x_{c}+x_{a}}{2}; \frac{y_{c}+y_{a}}{2})=(0;1)$
$x_{c}-4=0$ , $x_{c}=4$
$y_{c}+2=2$ , $y_{c}=0$

4) Координаты точки В(7/11; 39/11):
AB∧BD=B
$4x+1=\frac{10+x}{3}$
$x+10=12x+3$
$x_{B}= \frac{7}{11}$
$y_{B}=4*\frac{7}{11}+1=\frac{39}{11}$

5) Уравнение стороны $BC=- \frac{39}{37}x+ \frac{156}{37}$ :
B∈BC, C∈BC
$\left \{ {{4k+b=0} \atop {\frac{7}{11}k+b=\frac{39}{11}}} \right.$

$\left \{ {{b=-4k} \atop {b=\frac{39}{11}-\frac{7}{11}k}} \right.$

$-4k=\frac{39}{11}-\frac{7}{11}k$
$-4k+\frac{7}{11}k=\frac{39}{11}$
$-44k+7k=39$
$k=-\frac{39}{37}$
$b=-4k=\frac{39*4}{37}=\frac{156}{37}$

6) Координаты точкиD(-7/11; -17/11):
т. $O( \frac{x_{D}+x_{B}}{2}; \frac{y_{D}+y_{B}}{2})=(0;1)$
$x_{D}+\frac{7}{11}=0$ , $x_{D}=-\frac{7}{11}$
$y_{D}+\frac{39}{11}=2$ , $y_{D}=-\frac{17}{11}$

7) Уравнение стороны $AD=-\frac{39}{37}x-\frac{82}{37}$
A∈AD, D∈AD
$\left \{ {{-4k+b=2} \atop {-\frac{7}{11}k+b=-\frac{17}{11}}} \right.$

$\left \{ {{b=2+4k} \atop {-7k+11b=-17}} \right.$

$-7k+22+44k=-17$
$37k=-39$
$k=-\frac{39}{37}$
$b=2+4k=2-\frac{4*39}{37}=-\frac{82}{37}$

8) Уравнение стороны $DC=\frac{1}{3}x-\frac{4}{3}$
D∈DC, C∈DC
$\left \{ {{4k+b=0} \atop {-\frac{7}{11}k+b=-\frac{17}{11}}} \right.$

$\left \{ {{b=-4k} \atop {-7k+11b=-17}} \right.$

$-7k-44k=-17$
$-51k=-17$
$k=\frac{17}{51}=\frac{1}{3}$
$b=-\frac{4}{3}$

kalbim_zn (63.2k баллов) 05 Апр, 18