{ |3x - y + 2| <= 12<br>{ (x - 3a)^2 + (y + a)^2 = 3a + 4
Преобразуем первое неравенство в двойное
-12 <= 3x - y + 2 <= 12<br>-14 <= 3x - y <= 10<br>Или в систему
{ 3x - y >= -14
{ 3x - y <= 10<br>Отсюда
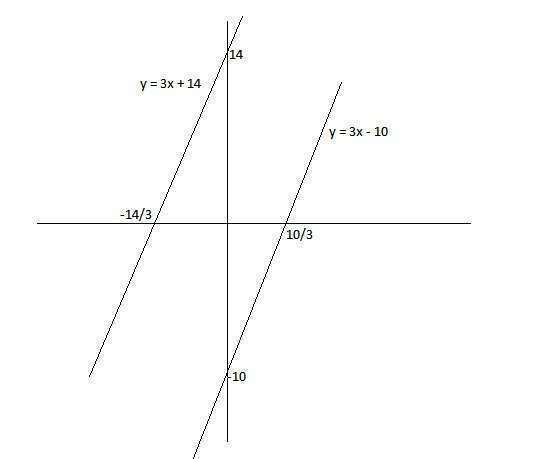
{ y <= 3x + 14<br>{ y >= 3x - 10
Это полоса между этими прямыми. Примерно показано на рисунке.
Второе уравнение - окружность с центром (3a; -a) и радиусом √(3a+4)
Если система имеет только одно решение, то одна из прямых является касательной к окружности.
1)
{ y = 3x - 10
{ (x - 3a)^2 + (y + a)^2 = 3a + 4
Подставляем
(x - 3a)^2 + (3x - 10 + a)^2 = 3a + 4
x^2 - 6ax + 9a^2 + 9x^2 - 60x + 100 + 6ax - 20a + a^2 = 3a + 4
10x^2 + 10a^2 - 60x + 100 - 20a = 3a + 4
10(x^2 - 6x + 9) + 10(a^2 - 2a + 1) = 3a + 4
10(x - 3)^2 + 10(a - 1)^2 = 3a + 4
(x - 3)^2 + (a - 1)^2 = (3a + 4)/10 = 0,3a + 0,4
Получаем квадратное уравнение относительно а
a^2 - 2a + 1 - 0,3a + (x - 3)^2 - 0,4 = 0
a^2 - 2,3a + (x - 3)^2 + 0,6 = 0
Находим два значения а, зависящие от х
2)
{ y = 3x + 14
{ (x - 3a)^2 + (y + a)^2 = 3a + 4
Решается точно также.