В равнобедренном треугольнике ABC(AB = BC) боковая сторона делится точкой касания...

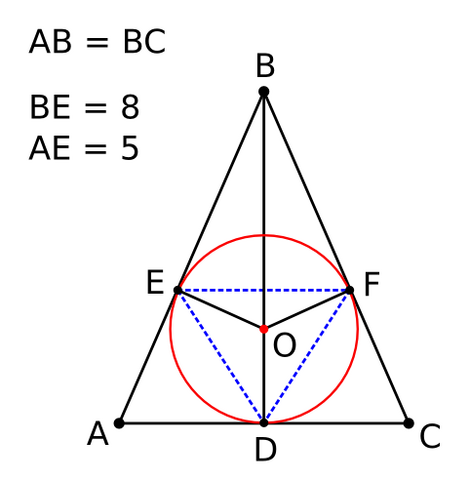
(Смотри фигуру во вложении.)

По определению, вписанная в треугольник окружность — это окружность, которая касается всех сторон треугольника. Используя свойство отрезков касательных к окружности, проведённых из одной точки: "если к одной и той же окружности из одной и той же точки проведены две касательных, то отрезки касательных от этой точки до точек касания будут равны", получим, что

$AE = AD = 5$ — это половина стороны основания.

Боковая сторона:

$AB = BC = AE + BE = 13$

Высота BD треугольника:

$BD = \sqrt{AB^2 - AD^2} = \sqrt{144} = 12$

Площадь треугольника ABC:

$S = 2 \cdot \left(\frac{1}{2} \cdot AD \cdot BD\right) = 5 \cdot 12 = 60$

Ответ: 60.