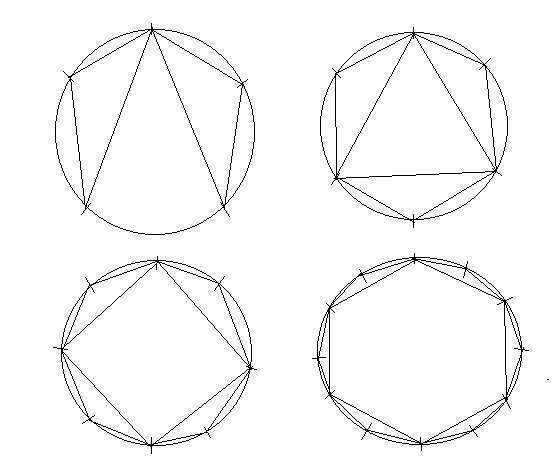
Сложная задача, и возможно, мне ее завернут за неправильное решение.
5 точек дают 2 треугольника, 6 - 3, 8 - 4, 12 - 6.
Первые 3 точки дают 1 треугольник, каждые следующие 2 точки - еще 1.
Можно предположить, что 999 точек дадут 1 + (999-3)/2 = 499 треугольников.