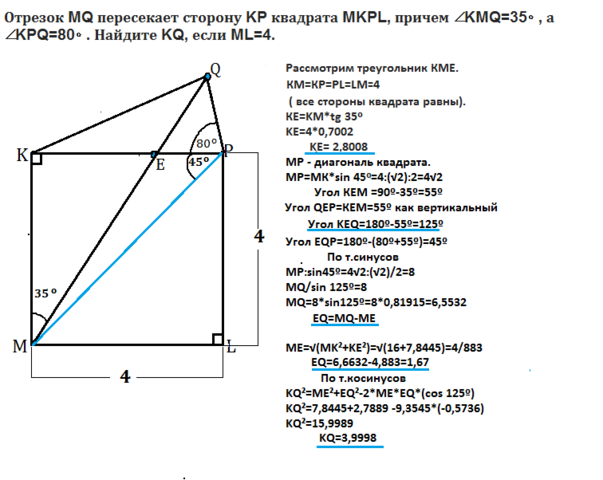
Рассмотрим рисунок, данный в приложении.
MKPL - квадрат.
Сумма острых углов прямоугольного треугольника 90º
Угол КЕМ =90º-35º=55º
Рассмотрим треугольник КМЕ. КМ=КР=РL=LM=4 ( все стороны квадрата равны).
КЕ=KM*tg 35º
KЕ=4*0,7002
KЕ= 2,8008
МР - диагональ квадрата.
МР=МК*sin 45=4:(√2):2=4√2
Угол QEP=КЕМ=55º как вертикальный
Угол KEQ=180º-55º=125º
Угол ЕQP=180º-(80º+55º)=45º
.........По т.синусов
MP:sin45º=4√2:(√2)/2=8
MQ:sin 125º=8
MQ=8*sin125º=8*0,81915=6,5532
EQ=MQ-ME
ME=√(MK²+KE²)=√(16+7,8445)=4,883
EQ=6,6632-4,883=1,67
.........По т.косинусов
KQ²=ME²+EQ²-2*ME*EQ*(cos 125º)
KQ²=7,8445+2,7889 -9,3545*(-0,5736)
KQ²=15,9989
KQ=3,9998