Номер 3 под цифрой 6,номер 8 под чифрой 1 и 10 под цифрой 1 пожалуйста

$3.6) \frac{16}{ x^{2} +5x-6} - \frac{20}{ x^{2} +5x+6} =1$
Замена переменной
$x^{2} +5x=t$
$\frac{16}{ t-6} - \frac{20}{ t+6} =1 \\ \\ \frac{16}{ t-6} - \frac{20}{ t+6} -1=0 \\ \\ \frac{16(t+6)-20(t-6)-(t-6)(t+6)}{ (t-6)(t+6)} =0 \\ \\ \frac{16t+96-20t+120-t ^{2} +36}{ (t-6)(t+6)} =0 \\ \\ \frac{-t ^{2}-4t +252}{ (t-6)(t+6)} =0 \\ \\ \left \{ {-t ^{2}-4t +252 =0 } \atop {(t-6)(t+6) \neq 0}} \right.$
-t²-4t+252=0
t²+4t-252=0
D=(-4)²-4·(-252)=16(1+63)=16·64=1024=32²
t=(-4-32)/2=-18    или    t=(-4+32)/2=14
$x^{2} +5x=-18$ $x^{2} +5x=14$
x²+5x+18=0 x²+5x-14=0
D=25-72<0 D=25+56=81<br>корней нет х=-7 или х=2
Ответ. -7; 2
8.1)
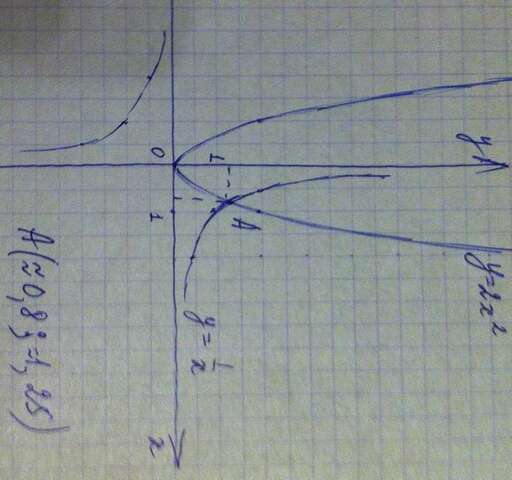
Парабола у=2х² пересекается с гиперболой $y= \frac{1}{x}$
в одной точке А ( см рисунок в приложении)
А(≈0,8; ≈1,26)

10.1)
$\left \{ {{ x^{2} -2x-15 \leq 0} \atop { x^{2} -12x+27\ \textless \ 0}} \right.$
Находим корни первого квадратного трехчлена
D=4+60=64
x₁=(2-8)/2=-3 или x₂=(2+8)/2=5
   + - +
----------[-3]-------------------------[5]---------
   \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Находим корни второго квадратного трехчлена
D=144-4·27=36
x=₃=3 x₄=9
   + - +
-----------(3)------------------(9)--------------
   /////////////////////////
Решение системы - пересечение найденных промежутков.
Ответ. (3; 5]