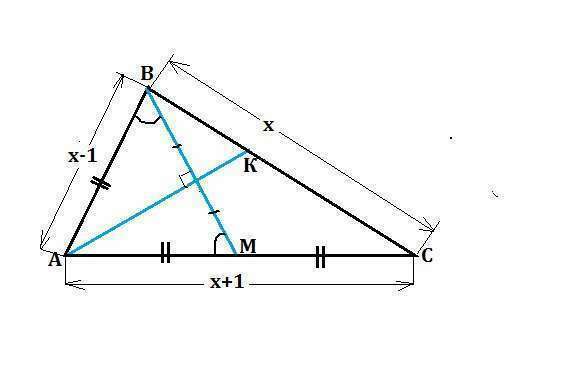
Пусть АК - биссектриса треугольника АВС , ВМ - его медиана.
Т.к. биссектриса треугольника АВМ перпендикулярна стороне ВМ, она является его высотой.
Если биссектриса треугольника совпадает с высотой, она является и его медианой,⇒
треугольник ВАМ - равнобедренный.
АВ=АМ.
ВМ - медиана треугольника АВС, ⇒
АВ=АМ=МС, и
АС=2 АВ.
Пусть средняя по длине сторона равна х
Если предположить, что АВ - средняя сторона, то
АС=х+1, ВС=х-1
Тогда АС=2х=х+1, откуда х=1, и ВС=1-1=0, чего быть не может. ⇒
ВС- средняя сторона.
ВС=х, АС=х+1, АВ=х-1
АС=2(х-1)=2х-2
2х-2=х+1 ⇒
х=3
ВС=3
АВ=3-1=2
АС=3+1=4 - это наибольшее значение самой длинной стороны