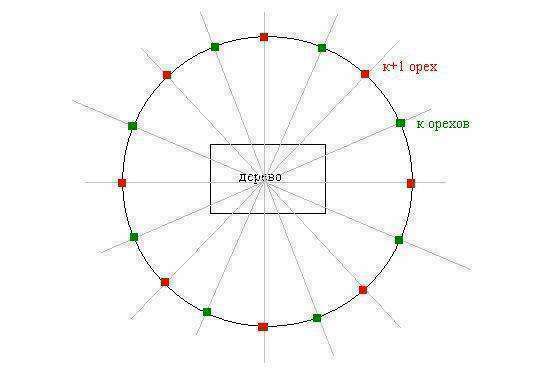
Я думаю так:
Раз 16 белок стоят вокруг дерева, то нет первой и последней белки (каждая белка может считаться 1-ой). У любых двух соседних белок количество орехов должно отличаться на 1 шт.
Если мы расставим 16 белок в круг, то у 8 белок должно быть орехов на 1 меньше, чем у других 8 (при этом, белки чередуются).
Пусть наименьшее число орехов у одной белки равно k, тогда:
8k + 8(k+1) = 55 орехов, k∈Z (целое число)
8k + 8k + 8 = 55
16k = 55 - 8 = 47
k = 47/16 - не является целым числом.
P.S. Для иллюстрации задачи прикрепляю картинку
Ответ: нельзя распределить орехи в соответствии с условием