Эту задачу можно решить разными способами. Один способ дан в первом решении.
Пусть данный треугольник будет АВС,
ВН- высота к основанию.
АК - высота к боковой стороне.
В прямоугольном треугольнике СВН катет ВН относится к гипотенузе СВ как 4:5, ⇒
Δ СВН - египетский и СН=3 ( то же получится и по т. Пифагора)
1.
Проведем НМ перпендикулярно ВС
Δ ВНС ~ Δ НМС - прямоугольные с общим углом при С.
Из подобия НС:ВС=МН:ВН⇒
3:5=МН:4 ⇒
МН=2,4
В равнобедренном треугольнике АВС высота и медиана ВН делит АС пополам.
В треугольнике АКС отрезки АН=НС,
МН параллельна АК ⇒
МН средняя линия △АКС
АК=2 МН=2*2,4=4,8
-------
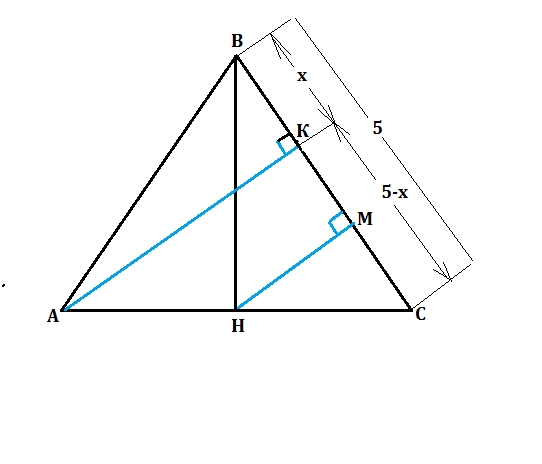
2. Пусть ВК=х, тогда КС=5-х.
АК²=АВ²-ВК²
АК²=АС²-КС²
АВ²-ВК²=АС²-КС²
25-х²=36-25+10х-х²
10х=50-36=14
х=1,4
АК²=АВ²-ВК²
АК=√( 25-1?96)=4,8