Первое неравенство
х²+у²-2у≤3
преобразуем получим
х²+(у-1)²≤4
множество точек внутри окружности с радиусом 2 и центром в (0;1) и сама окружность
второе неравенство
2|x|+|y-1|≥2
сначала построим график функции
2|x|+|y-1|=2
при х>0
y>1
y=3-2x
при х>0
y<1<br>y=2x-1
при x<0<br>y>1
y=2x+3
при х<0<br>y<1<br>y=-2x-1
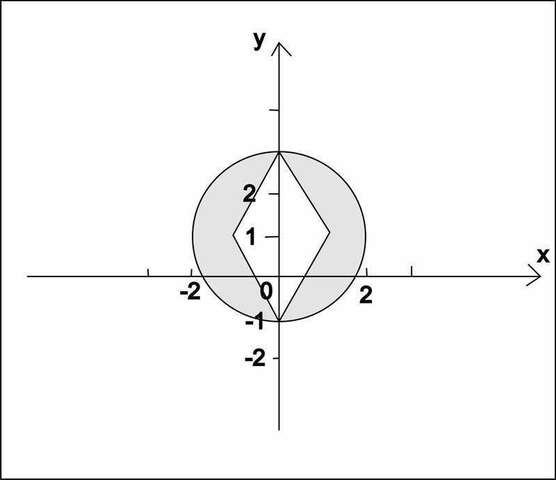
после построения этих 4 графиков получаем ромб с вершинами (-1;1) (0;3) (1;1) (0;-1)
решением неравенства
2|x|+|y-1|≥2
является множество точек за пределами данного ромба и сам ромб
графики показаны на рисунке
S(окружности)=πR²=4π
S(ромба)=2·2=4
S(получившейся фигуры)=4π-4