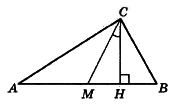
Из подобия треугольников АВС и НСВ следует, что ∠ В=∠НСА.
Медиана, проведенная из вершины прямого угла, равна половине гипотенузе. Значит треугольник МВС – равнобедренный, и ∠ВСН=∠В=∠НСА.
∠НСА+∠ВСН=90°–∠МСН=90 °–20 °=70°; ∠НСА=70:2=35°.
∠А=90°–∠НСА=90°–35°=55°.
ОТВЕТ: 55°
рисунок смотри на фото