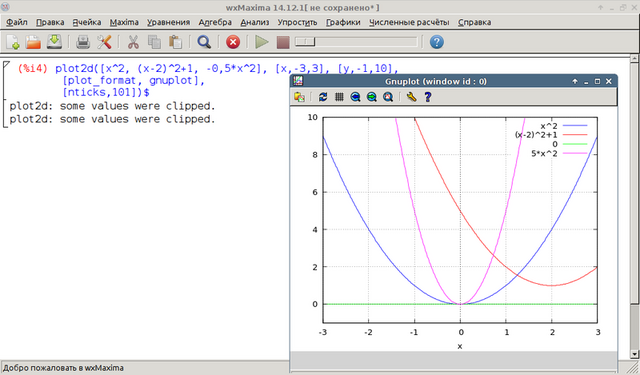
Ну алгоритм не алгоритм, а принцип построения поясню.
Во первых слева дополнительное слагаемое +1 "сдвигает" график исходной функции  на одну единицу вверх вдоль (параллелно) оси OY. График "поднимается" .
на одну единицу вверх вдоль (параллелно) оси OY. График "поднимается" .
(Если бы было -1, график исходной функции сдвинулся бы на 1 вниз).
Вообще,чтобы получить график функции f(x)+B, исходный график нужно сместить на B единиц вверх (при B>0), или вниз ( при B<0).</em>
Далее
График функции y=f(x+C) получается из исходного графика функции y=f(x) путем сдвига его вправо (С<0) или влево (C>0) на C единиц.
Т.е. в нашем случае нам нужно сдвинуть исходный график y=x^2 на 1 единицу вверх и на 2 единицы вправо.
Ну и коэффициент a при х^2 "растягивает" или "сжимает" график к вертикальной оси.
Может даже "Зеркально отразить" исходный график (при a=-1).
Чтобы из исходного графика y=x^2 получить график y=a*x^2
нужно координаты всех его точек (на практике только нескольких опорных пересчитать по следующему принципу
(x, a*x^2). Т.е координата X, выбранной точки не меняется, а координату Y надо умножить на a.
P.S. В свое время в учебниках что-то подобное писали, недавно я встречал подобные и более подробные рассуждения в книге:
Зельдович Я. Б. "Высшая математика для начинающих и ее приложения к физике"