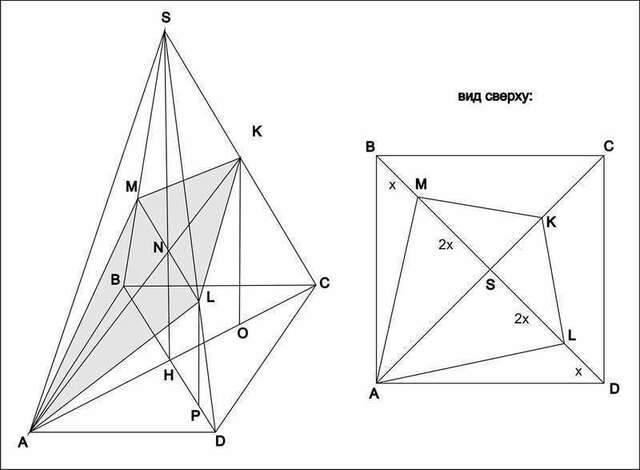
Треугольники ANH и AKO подобны => NH=(2/3)KO=LP
из подобия треугольников HSD и PLD находим что LD=(1/3)SD
HP=(2/3)HD
по теореме Пифагора
AC=12=BD
ML=(2/3)BD=8
S(сечения)=(1/2)*AK*ML=60
AK=15
по теореме Пифагора для АКО
КО=12
NH=8
рассмотрим треугольник ANH, проведём в нём высоту из H на AN
из подобия образовавшихся треугольников находим эту высоту h
h=4,8
эта высота и будет расстоянием от точки В до плоскости сечения тк BD параллельна сечению