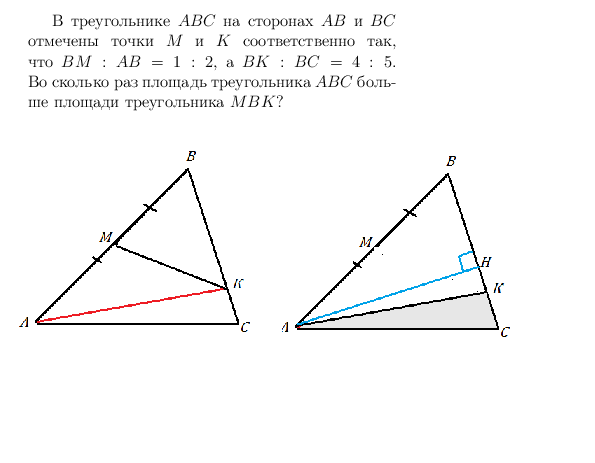
В треугольнике АВС на сторонах АВ и ВС отмечены точки М и К соответственно так, что ВМ:АВ=1:2, а ВК:ВС=4:5. Во сколько раз площадь треугольника АВС больше площади треугольника МВК?
Решение.
Соединив А и К, получим два треугольника с равной высотой АН из А к ВС.
Если высоты двух треугольников равны. то их площади относятся как основания.
ВК
:ВС=4
:5
Площадь треугольника АКВ равна 4/5 площади треугольника АВС.
В треугольнике АВК отрезки ВМ:АВ=1:2, т.е. ВМ=АМ. ⇒
МК- медиана и делит треугольник АВК на два равновеликих ( равных по площади).
Площадь треугольника ВМК равна 0,5*4/5=
2/5 S ∆ АВС
S∆ ABC: 2/5 S ∆ АВС=2,5
Ответ: Площадь ∆ ABC больше площади ∆ АВС в 2,5 раза.