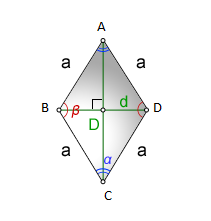
По теореме Пифагора находим одну из сторон ромба а. По скольку острый угол равен 60, а большая диагональ будет являться биссектрисой угла. Мы получим 4 прямоугольных треугольника (см. рисунок), где по теореме: против угла в 30 градусов лежит катет равен половине гипотенузу, гипотенуза это и есть наша а, а катет половина меньшей диагонали (BD/2 = 1.5), т.е. а = 1.5*2 = 3. Далее воспользуемся формулой для нахождения площади:
S = a^2sin(α) = 3^2 sin (120) = 9*(корень из 3)/2