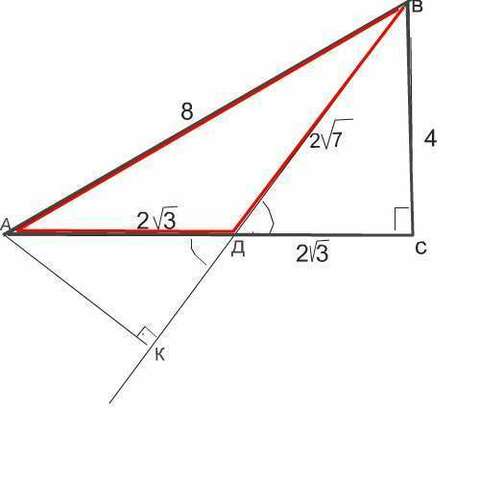
Данный треугольник АВС - прямоугольный,
АВ - гипотенуза,
АС и ВС - катеты.
На эту мысль наводит отношение длин катетов и стороны АВ.
ВС=АВ:2
Если предположение верно, то данное ниже равенство будет верным:
АС=√(АВ²-ВС²)
Подставим известные значения сторон:
4√3 =√(64-16)
√(64-16)=√48=4√3
Итак, мы доказали, что треугольник АВС прямоугольный.
Продолжим прямую ВД за АС и проведем к ней перпендикуляр.
Он равен расстоянию от А до ВД и является высотой треугольника АВД.
Точку пересечения обозначим К.
Если в прямоугольных треугольниках острый угол одного равен острому углу другого, то такие треугольники подобны.
Углы при Д в них вертикальные и потому равны.
Углы АКД=ВСД=90°
Δ АДК и Δ ВСД подобны.
АД=ДС по условию задачи.
АД и ДВ - гипотенузы этих треугольников.
В треугольнике АКД известна сторона АД.
В треугольнике ВСД известны два катета.
Найдем ВД по теореме Пифагора:
ВД²=ВС²+ДС²
ВД =√(16+12)=√28=2√7
ВД:АД=ВС:АК
(2√7):2√3=4:АК
8√3=2АК ·√7
АК=4√3:√7
АК является высотой треугольника АВД, проведенной к стороне ВД и в то же время расстоянием от А до ВД.
S АВД=2√7·4√3·√7 =8√3 см²
Расстояние от А до ВД=АК=(4√3:)√7