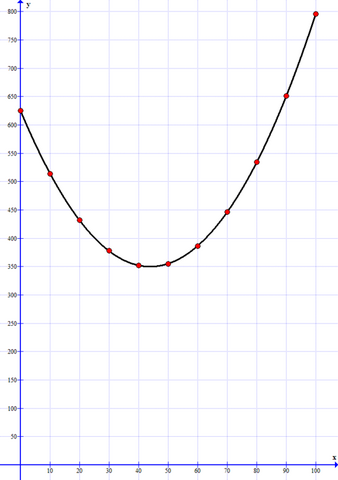
Можно решать графически, нарисовав график зависимости суммарной площади от периметра одной из фигур (например, круга).
Периметр фигуры- это и есть длина куска проволоки, взятой для изготовления этой фигуры. Длину для удобства будем выражать в сантиметрах (т.е. длина проволоки будет 100см).
Обозначим периметр круга как x (икс)
Тогда периметр квадрата будет равен оставшемуся куску проволоки, то есть: 100-x
Периметр круга равен два пи, умножить на радиус (  ).
).
Отсюда, радиус равен: 
Площадь круга равна пи умножить на радиус в квадрате: 
Периметр квадрата равен четырём его сторонам (  ).
).
Отсюда, сторона равна: 
Площадь квадрата равна: 
Теперь, запишем чему равна сумма площадей круга и квадрата:

Как видим, получилось уравнение параболы, у которой ветви направлены вверх (так как коэффициент при икс квадрат- положительный).
Если поразмыслить, то мы поймём, что у такой параболы максимальное значение y для любого отрезка по x будет на одном из концов этого отрезка (на том, который дальше от вершины параболы).
Подтвердим это, построив график функции 
Для начала, вычислим несколько значений функции при разных икс:
x y
0 795,8
10 650,8
20 534,3
30 446,2
40 386,5
50 355,2
60 352,3
70 377,9
80 431,8
90 514,2
100 625,0
Затем, по этим точкам построим график (смотри приложенный рисунок).
По графику видно, что максимальное значение суммарной площади получается при x=100 (хотя, это видно и без графика, по вычисленным значениям функции).
Значит, длина первой части проволоки (для изготовления круга) нужна 100 сантиметров (т.е. 1 метр), а длина второй части- для квадрата получится равной: 100-x = 100-100 = 0см.
То есть максимальная площадь получится, если квадрат вообще не делать, а всю проволоку пустить на изготовление круга.