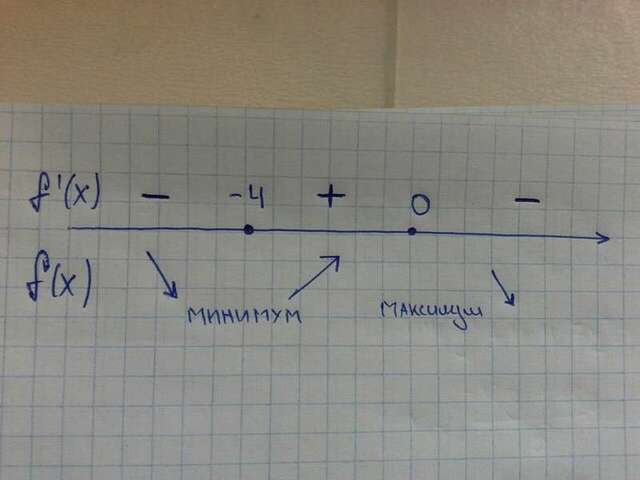1)Найдите точку экстремума функции: y=-x³/3-2x²+3 и определить их характер: 2)Решите...

Question

Дан 1 ответ

Правильный ответ

$1)y=-\frac{x^3}3-2x^2+3$

Для того, чтобы найти точки экстремума(точки минимума или максимума) нам нужно найти производную и приравнять ее к 0.

(Почему так? Как это работает?
Производная - скорость роста функции. Если значения производной отрицательны, то функция убывает. Если же значения производной положительны, то функция возрастает. Есть точки, в которых функция ни возрастает, ни убывает. В этих точки график производной проходит через ось Ох, то есть значение производной равно 0.)

$y'=(-\frac{x^3}3-2x^2+3)'=(-\frac{x^3}3)'-(2x^2)'+(3)'=-x^2-4x$
$y'=0\\-x^2-4x=0\\x^2+4x=0\\x(x+4)=0\\x=0,x=-4$

$x=0,x=-4$ - точки экстремума.

Для того, чтобы определить, где точка минимума, а где точка максимума нужно нарисовать координатную прямую, отметить на ней точки и определить знаки интервалов(как в методе интервалов). (см. рисунок)
Для того, чтобы определить знак интервала, подставляем любое значение из этого интервала в уравнение производной.

Пример: определим знак интервала $(0;+\infty)$
Возьмем число: 1.
$y'=-x^2-4=-1-4=-5\ \textless \ 0$
Интервал отрицательный и т.д.

Там, где интервалы отрицательны(где отрицательны значения производной) сама функция убывает.
Там, где интервалы положительны, функция возрастает. (Таким методом определяют промежутки возрастания и убывания функций)

И так. Если функция сначала убывала, а потом проходя через какую-то точку начала возрастать, то, очевидно, она прошла через точку минимума. (см. рисунок)
Если же возрастание меняется убыванием это, очевидно, точка максимума.

И так:
$x=0$ - точка максимума.
$x=-4$ - точка минимума.

Прошу обратить внимания, что для точек минимума и максимума не нужно искать значение функции в это точке, и не стоит записывать ее координаты так: (0;2) и тому подобное. Правильная запись выше.

$2)\sqrt{x^2-1}=\sqrt{3}\\\sqrt{(x^2-1)^2}=\sqrt{(3^2)}\\x^2-1=3\\x^2=4\\x=б2$

аноним 03 Апр, 18