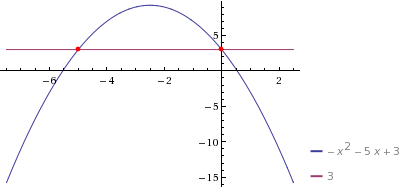
строим графики (во вложениях)
смотрим точки их пересечения.
их также можно найти, приравняв уравнения этих графиков

точки пресения 0 и -5.
Площадь фигуры находится интеграл от разностей графиков: из уравнения графика, который выше, вычетается график тот что ниже.
получается, что (-x^2-5x+3-3) будет под интегралом. пределы интегрирования - точки пересечения графиков: