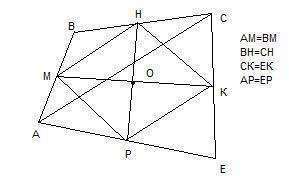
В выпуклом АВСЕ построим диагональ АС. Рассмотрим получившийся треугольник АВС. Здесь МН - средняя линия, т.к. по условию она соединяет середины сторон АВ и ВС. Значит
МН II АС, МН=1/2АС
Рассмотрим треугольник АЕС. Здесь РК - средняя линия, т.к. по условию она соединяет середины сторон АЕ и СЕ. Значит
РК II АС, РК=1/2АС. Следовательно,
МН II РК, МН = РК.
Таким образом, в четырехугольнике МНКР две стороны равны и параллельны, значит МНКР - параллелограмм. Диагонали параллелограмма МК и НР точкой пересечения О делятся пополам (МО=КО, РО=НО), что и требовалось доказать.