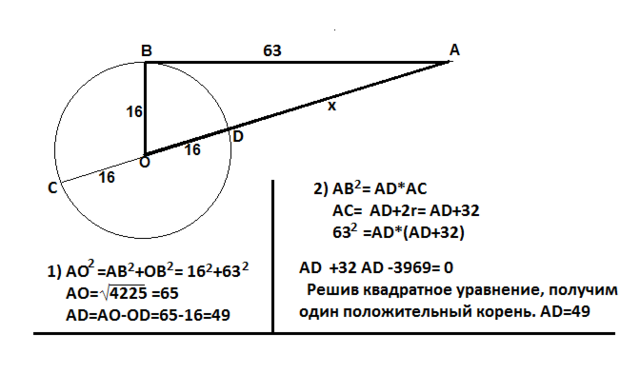
Решить задачу можно двумя способами. Всегда предпочтительнее более простое и короткое решение.
1) Радиус,проведенный в точку касания, образует с касательной прямой угол.
По т.Пифагора в прямоугольном треугольнике АВО гипотенуза
АО²=АВ²+ВО²
АО²=3969+256=4225=169*25 ( это разложение на множители числа 4225)
АО=√169*√25=13*5=65
АD=АО-ОD=65-16=49
-------
По теореме о секущей и касательной, проведенных из одной точки, квадрат касательной равен произведению секущей на её внешнюю часть.
АВ²=AD*AC
AC=AD+CD=AD+32.
Решение получившегося в результате необходимых действий квадратного уравнения даст два корня: 49 и -81. Второй не подходит.
AD=49.