Ну можно например так. Немного только достроить.
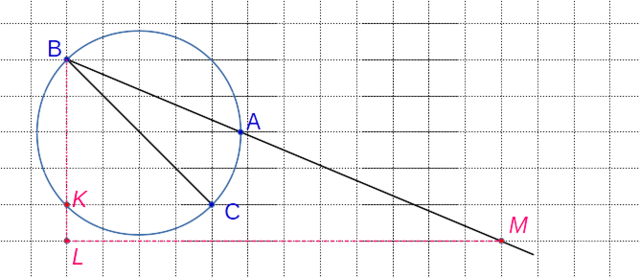
Сразу видно, что угол KBC 45°
Далее из треугольника LBM найдем угол при вершине B
 (1)
(1)
По теореме Пифагора найдем BM

Тогда подставим в (1) BM=13, BL=5

Ну а требуемый угол ABC = LBM-KBC≈67,38^o-45^o=22,38^o
Естественно ответ приближенный.
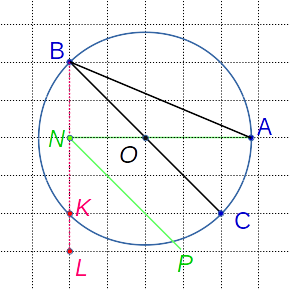
Можно иначе. зеленое построение на втором рисунке. При этом NP строится параллельно AB
угол BON=45°, ONP=BON как накрест лежащие при параллельный прямых BC, NP и секущей NA. Углы ONP=AOC=45° как соответственные при параллельных прямых BC, NP и секущей NA.
Углы BOA и AOC смежные, поэтому BOA=180-AOC=180-45=135°
Далее треугольник AOB равнобедренный OA=OB как радиусы окружности.
Тогда угол ABC=(180°-BOA)/2=(180°-135°)/2=45°/2=22,5°
Ну да, пожалуй так точнее.