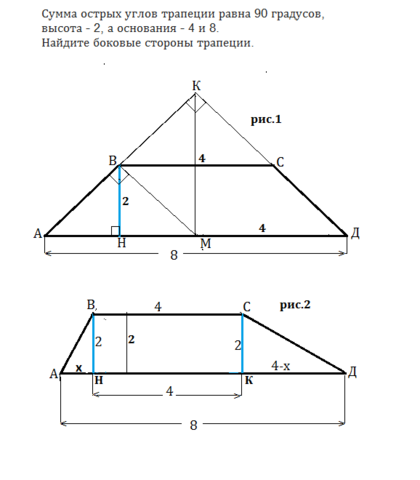
Достроим трапецию АВСД до треугольника с вершиной К. (см.рис.1 приложения)
Сумма острых углов этого треугольника по условию равна 90º, следовательно, угол АКД=90º и этот треугольник - прямоугольный.
ВС|| АД
ВС=4=АД:2 и для треугольника АКС является средней линией.
Тогда высота КМ треугольника АКД равна 2*ВН=4 и равна половине гипотенузы АД.
Медиана прямоугольного треугольника, проведенная из прямого угла, равна половине гипотенузы.
Если высота и медиана прямоугольного треугольника равны, то высота является его медианой и этот треугольник равнобедренный.
КМ=АМ.
Проведем ВМ|| СД, треугольник АВМ равнобедренный прямоугольный, АН=ВН=2 и его углы равны углам при основании трапеции, т.е. равны 45ª
Гипотенуза равнобедренного прямоугольного треугольника равна его катету, умноженному √2, что можно вычислить и по т.Пифагора, и по формуле
с=а:sin 45ºα, где с-гипотенуза]. а - катет, α - противолежащий ему острый угол. ⇒
АВ=СД = 2√2
------------
Боковые стороны трапеции с известными основаниями и высотой можно найти и другим способом.
Рассмотрим рис.2 приложения.
Высоты ВН и СК "высекают" из основания АД отрезок НК=ВС и
АН+КД=8-4=4
Если принять АН=х, то КД=4-х.
Высоты ВН=СК.
Из прямоугольных треугольников АНВ и СКД по т.Пифагора выражается квадрат высоты, эти значения приравниваются и из получившегося квадратного уравнения находится х.
Затем его значение подставляется для нахождения по т.Пифагора гипотенузы этих треугольников и таким образом находятся боковые стороны трапеции. Этих вычислений я приводить не буду, но Вы можете их проделать и для данной в условии трапеции найдете х=2.
Т.е. АН=ВН.