Решите
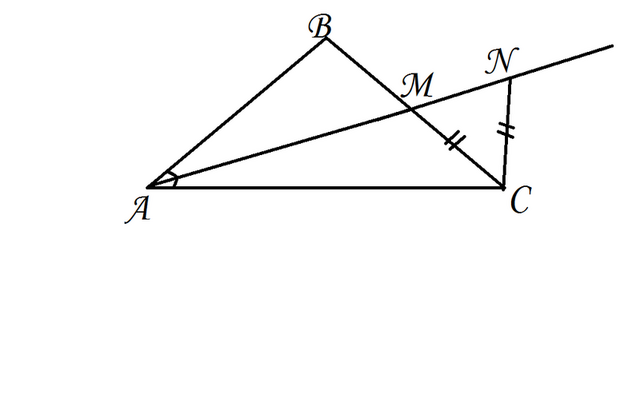
1. Доказать, что биссектриса внутреннего угла А треугольника АВС делит противоположную сторону на отрезки, пропорциональные сторонам АВ и АС. АС/АВ=МС/ВМ. Указание: Для доказательства построим на АМ точку N такую, что СМ=СN. (СМ во влажения)
2. Решить уравнение

3. Дидона, сестра царя Тира, собиралась огородить веревкой длины 240 м участок земли, имеющий форму круга. Однако веревка случайно порвалась на две части так, что суммарная площадь двух непересекающихся круглых участков, огороженных получившимися кусками веревки, уменьшилась в 1,6 раза по сравнению с первоначальной. Найти длину каждого из кусков веревки.
4. Четыре параллели, между которыми последовательные расстояния относятся, считая сверху 2:3:4, пересечены двумя сходящимися прямыми. Из полученный параллельных отрезков крайние равны 60 и 96. Определить средние отрезки.