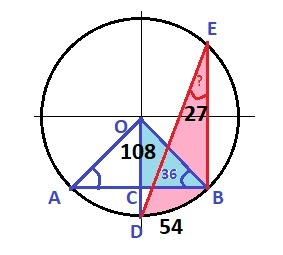
Рисунок к задаче в приложении.
ДАНО
АС=СВ
∠АВО = 36°
НАЙТИ
∠BED=?
РЕШЕНИЕ
Из условия АС=СВ и АО=ОВ следует, что ΔАОВ - равнобедренный и ∠ОАВ = ∠АВО = 36°.
Сумма углов ΔАОВ = 180°.
∠АОВ = 180° - 2*36° = 180° - 72° = 108° - центральный угол.
Прямая AD, как продолжение высоты ОС делит дугу АВ поровну.
∠BOD = 108° : 2 = 54°.
∠BED - вписанный и равен половине центрального угла дуги на которую он опирается.
∠BED = 1/2*∠BOD = 54° : 2 = 27° - ОТВЕТ