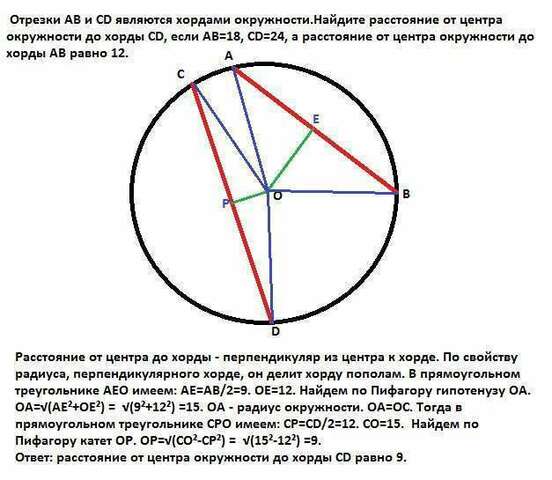
Расстояние от центра до хорды - перпендикуляр из центра к хорде. По свойству радиуса, перпендикулярного хорде, он делит хорду пополам. В прямоугольном треугольнике АЕО имеем: АЕ=АВ/2=9. ОЕ=12.
Найдем по Пифагору гипотенузу ОА. ОА=√(АЕ²+ОЕ²) = √(9²+12²) =15.
ОА - радиус окружности. ОА=ОС. Тогда в прямоугольном треугольнике СРО имеем: СР=СD/2=12. СО=15.
Найдем по Пифагору катет ОР. ОР=√(СО²-СР²) = √(15²-12²) =9.
Ответ: расстояние от центра окружности до хорды СD равно 9.