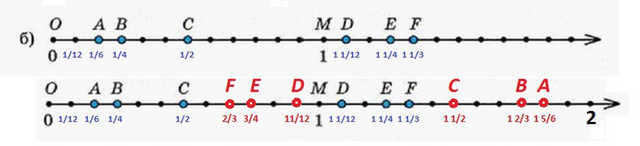
Дан координатный луч. Единичный отрезок равен 12. Это значит, что каждое деление равно = 1/12.
1.
Определяем координаты точек на луче.
A= 2/12 = 1/6, B = 3/12 = 1/4? C = 6/12= 1/2, M=1 (дано),
D = 1+1/12 = 1 1/12, E = 1 1/4, F = 1 1/3 - выполнено.
2.
Определяем координаты симметричных точек относительно точки М(1) (на рисунке отмечены красным цветом, хотя в математике обозначают штрихом " А' ").
КАК? - Отражаем, как в зеркале, которое стоит на букве М.
Расстояние от М до А = М(1) - А(1/6) = 5/6.
Для симметричной точки A' = М(1) + 5/6 = 1 5/6
Сразу для точки С'. СМ= 1-1/2 = 1/2 С' = M+CM = 1 1/2.
Остальные ответы на рисунке.