Если вспомнить, что величина, умноженная на корень из двух, это в то же время формула диагонали квадратаd=а√2 и гипотенузы равнобедренного прямоугольного треугольника, то нетрудно будет узнать величину искомого угла.
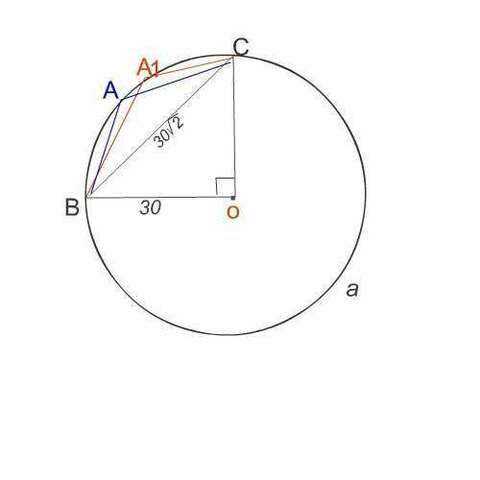
Соедимим концы В и С хорды с центром окружности.
Радиусы окружности и хорда образуют прямоугольный равнобедренный треугольник СОВ
( см. рисунок вложения).
Выбрав на дуге ВС произвольно точку А, соединим ее с В и С.
∠ ВАС вписанный и равен половине центрального угла ВаС.
∠ВаС=360°-90°=270°, следовательно,
∠ВАС=270°:2=135°
Отметим, что величина этого угла не зависит от местоположения точки Апо отношению к В и С.
∠ВАС=∠ВА₁С, как и любому углу, вершина которого будет лежать на этой же дуге, а концы угла опираться на дугу ВаС.