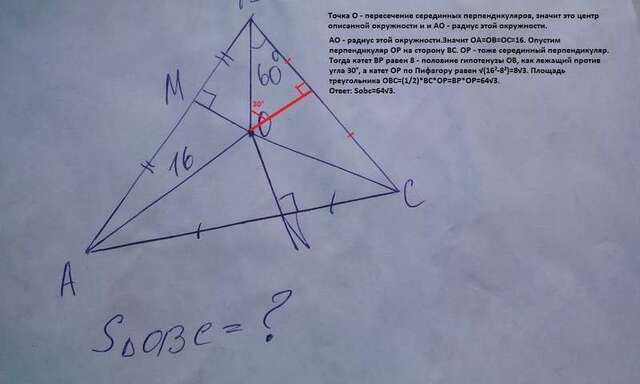
1) Точка О - пересечение серединных перпендикуляров, значит это центр описанной окружности и и АО - радиус этой окружности.Значит ОА=ОВ=ОС=16. Опустим перпендикуляр ОР на сторону ВС. ОР - тоже серединный перпендикуляр. Тогда катет ВР равен 8 - половине гипотенузы ОВ, как лежащий против угла 30°, а катет ОР по Пифагору равен √(16²-8²)=8√3. Площадь треугольника ОВС=(1/2)*ВС*ОР=ВР*ОР=64√3.
Ответ: Sobc=64√3.
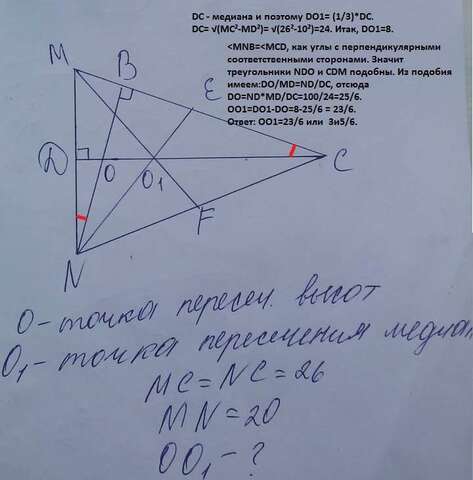
2)DC - медиана и поэтому DO1= (1/3)*DС.
DC= √(MC²-MD²)= √(26²-10²)=24. Итак, DO1=8.
DO=ND*MD/DC=100/24=25/6.
ОО1=DO1-DO=8-25/6 = 23/6.
Ответ: ОО1=23/6 или =3и5/6.