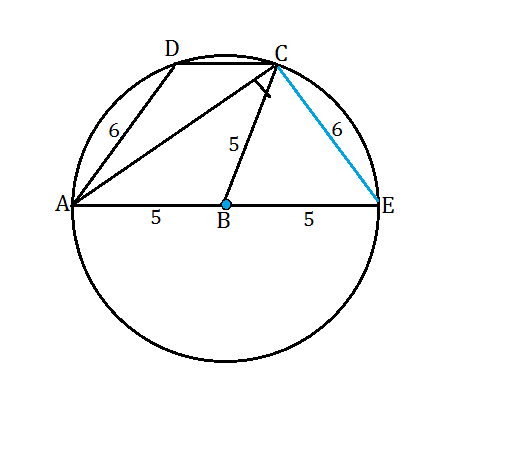
В - центр окружности. АВ - радиус. Продолжим его до пересечения с окружностью в точке Е.
АЕ-диаметр.
Соединим С и Е.
ADCЕ- трапеция, т.к. DC параллельна АЕ.
Эта трапеция - вписанная, а вписать можно только равнобедренную трапецию. Это следует из свойства вписанного четырехугольника ( сумма противоположных углов равна 180º, это и свойство равнобедренной трапеции).
⇒ СЕ=АD=6
АЕ=2r=10.
Угол АСЕ - вписанный, опирается на диаметр, ⇒ равен 90º.
В треугольнике АСЕ гипотенуза равна 10, один кает = 6, следоватеьно, он - египетский, второй катет АС=8 ( можно найти ипо т.Пифагора).
Ответ:АС=8