Решить с подробным решением._))

$\frac{x^2-5x+6}{x+1} \leq 0$

Подобные неравенства решаются методом интервалов. В этом методе мы находим все точки, в которых выражение(в данном случае и числитель и знаменатель) обращаются в 0. Потом эти точки отмечаем на прямой, и находим знаки интервалов. А от туда записываем ответ.
Итак, к делу:

$\frac{x^2-5x+6}{x+1} \leq 0$

Числитель:
$x^2-5x+6=0\\D=5^2-4*6=25-24=1\\\\x_1=\frac{5+1}2=\frac{6}2=3\\\\x_2=\frac{5-1}{2}=\frac{4}2=2$
В итоге, наше неравенство выглядит таким образом:

$\frac{(x-2)(x-3)}{x+1} \leq 0$

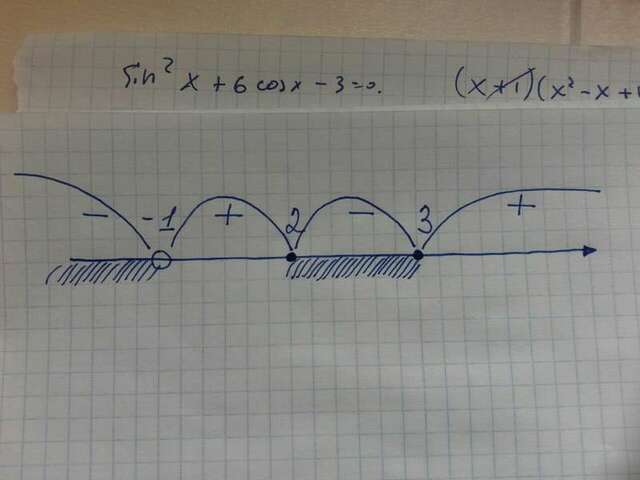
Теперь рисуем прямую, отмечаем точки и находим знаки промежутков. (см. рисунок)
Обратите внимание, что точка -1 "выколота", так при 1, в знаменателе получается 0, а на 0 делить нельзя.

В ответ записываем промежутки, в которых стоит знак -
$x\in(-\infty;-1)U[2;3]$
Произведение наибольшего отрицательного целого корня (-2) и наименьшего целого корня(2): $-2*2=-4$
Ответ: -4.