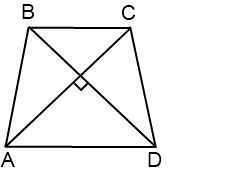
Рисунок на фото. (Допишешь точку О в месте пересечения диагоналей)
Дана равнобедренная трапеция АВСD.
АВ и СD - боковые стороны.
ВС - меньшее основание.
По свойствам равнобедренной трапеции АВ=СD=ВС
Проведем диагональ ВD. По условию ∠АВD=120°.Проведем вторую диагоняль СА. (точка их пересечения О)
ΔВСО равнобедренный (по свойствам равн. трапеции), где
ВО=ОС и ∠ ОВС=∠ ВСО = X.
ΔАВС тоже равнобедренный. У него АВ=ВС (по условию). А из этого следует, что ∠ВАС=∠ВСА(или ВСО), а значит ∠АВС=∠ВСО=∠ОВС =Х. Найдем чему равен Х:
120+Х это ∠АВС
120+Х+Х+Х=180°
3Х=60
Х=20°.
Следовательно, углы при меньшем основании = 120+20=140° (каждый по 140°)
Углы при большем основании = (360-140-140):2=40°(каждый по 40°)