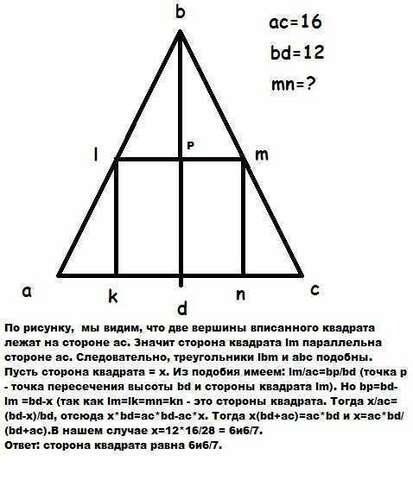
По рисунку, мы видим, что две вершины вписанного квадрата лежат на стороне ас. Значит сторона квадрата lm параллельна стороне ас. Следовательно, треугольники lbm и abc подобны. Пусть сторона квадрата = х. Из подобия имеем: lm/ac=bp/bd (точка р - точка пересечения высоты bd и стороны квадрата lm). Но bp=bd-lm =bd-x (так как lm=lk=mn=kn - это стороны квадрата. Тогда х/ас=(bd-х)/bd, отсюда х*bd=ас*bd-ас*х. Тогда х(bd+ас)=ас*bd и х=ас*bd/(bd+ас).В нашем случае х=12*16/28 = 6и6/7.
Ответ: сторона квадрата равна 6и6/7.