1. Найти площадь прямоугольного треугольника, гипотенуза которого равна 17 см, а один из...

Question

46 просмотров

1. Найти площадь прямоугольного треугольника, гипотенуза которого равна 17 см, а один из катетов - 8см.
2. Найти площадь трапеции, стороны которой равны 17, 10,5 и 10 см.
3. В прямоугольном треугольнике АВс катет СА=3см, угол А= 45градусов Найти гипотенузу АВ

Геометрия FelixWolf_zn (234 баллов) 03 Апр, 18 | 46 просмотров

Дан 1 ответ

2Stupid_zn · Answer 1 · 2018-04-03T13:36:17+0000

I. Найдем площадь прямоугольного треугольника.
1. Найдем второй катет.
с = 17 см,
a = 8 см.
Теорема Пифагора:
$c^{2} =a^{2} +b^{2} \\ b^{2} = c^{2} - a^{2} \\ b= \sqrt{c^{2} - a^{2}} \\ b= \sqrt{289-64}= \sqrt{225} =15$
b = 15 см
2. Найдем площадь прямоугольного треугольника.
$S= \frac{1}{2} ab \\ S= \frac{1}{2}*8*15=60$
Ответ: 60 см².
II. Найдем площадь трапеции.
$S= \frac{1}{2} (a+b)h$
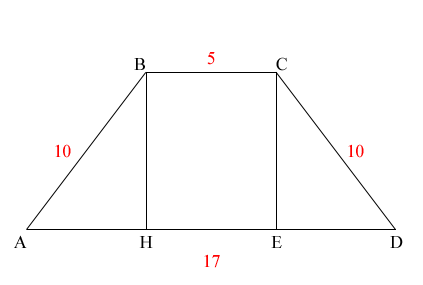
1. Найдем высоту трапеции из прямоугольного треугольника ABH.
Гипотенуза прямоугольного треугольника равна 10 см (см. рисунок).
Найдем катет AH.
$17-5=12$ (см) - сумма катетов AH и DE.
$AH= \frac{12}{2} =6$ (см).
Найдем теперь высоту BH.
$BH= \sqrt{100-36}= \sqrt{64} =8$ (см)
2. Найдем площадь трапеции:
$S= \frac{1}{2} (17+5)8=88$ (см²)
Ответ: 88 см²
III. Найдем гипотенузу AB.
$cos45= \frac{AC}{AB} \\ AB= \frac{AC}{cos45} \\ AB= \frac{3}{cos45} = \\ = \frac{3}{ \frac{1}{ \sqrt{2} } } =3 \sqrt{2}$
Ответ: 3√2 см