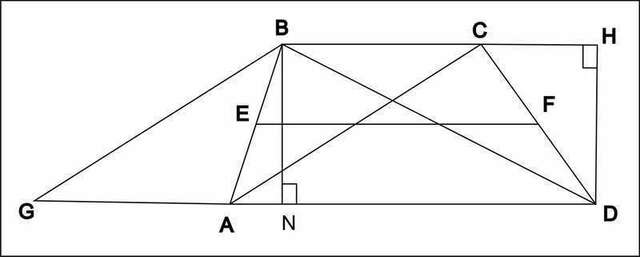
Пусть АВСD- данная трапеция
построим GB параллельно СА, GB=CA тк ВС параллельно AD
GA=BC
площадь треугольника равна половине высоты на основание
S (GBA)=S (BCD) тк BN=HD, GA=BC
=> S(GBD)=S(ABCD)
=> достаточно найти площадь GBD
EF=(BC+AD)/2=10
GD=BC+AD=20
по формуле Герона получаем
S=sqrt{p(p-a)(p-b)(p-c)}
где р-полупериметр
S=sqrt{p(p-АВ)(p-BD)(p-GD)}=sqrt{21*1*14*6}=42
Ответ:42