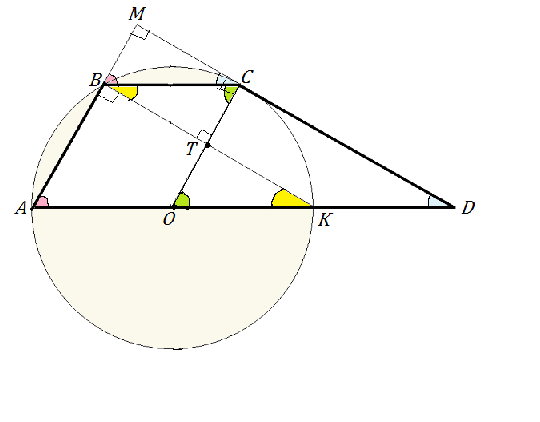
Продлим боковые стороны трапеции до пересечения в точке М.
Сумма углов при основании треугольника АМВ равна 90°, следовательно, угол АМD равен 180°-90°=90°
Рассмотрим треугольники АМD и BМC.
Так как ВС|| АD, соответственные углы при их пересечении секущими АМ и DМ равны. Рассматриваемые треугольники подобны по трем углам. Отсюда АМ:BМ=AD:BC
(10+BМ):BМ=18:6
6*(10+ВМ)=18 ВМ
60+6 ВМ=18 ВМ
12 ВМ=60
ВМ=5
Из С проведем СО параллельно АВ.
В четырехугольнике АВСО противоположные стороны параллельны, ⇒АВСО= параллелограмм, и АО=ВС=6 см, СО=АВ=10 см
Из вершины В проведем прямую ВК параллельно СD до пересечения с АD. ВМ=ТС=5 ( т.к. ВМСТ- прямоугольник из параллельности его сторон и равенства углов) ⇒
Т - середина ОС, который равен АВ,
угол ВСТ=углу ТОК как накрестлежащие.
Вертикальные углы при Т - равны.
Следовательно, ⊿ ВТС=⊿ ОТК по двум углам, прилежащим к равной стороне. ⇒
ОК=ВС=6
АО=ОК=6 см
Угол АВК вписанный и прямой, опирается на АК ⇒ диаметр, О - его середина. ⇒
R= АО=6 см
---------
Но так и напрашивается другое решение, при котором величина АВ как будто бы является лишней.
Если мы проведем ВК параллельно МD. то угол АВК - прямой, опирается на АК , и потому АК - диаметр. Поскольку DК=ВС=6, то АК=18-6=12, и тогда R=12:2=6 см)