Для начала видим, что у нас тут имеются некоторые ограничения на переменную, что необходимо обязательно учесть. По моей практике, очень многие не учитывают ОДЗ уравнения, и в ответ пишут всё "как есть". Это грубая ошибка. Поэтому этап первый в решении нашего уравнения - записать область допустимых значений уравнения.
1)Просто смотрим на проблемные места уравнения(квадратные корни и прочее) и выписываем всё, что нам попадётся на пути.
sin x >= 0
sin x не равен 0
cos x не равен 0
Первое условие понятно, откуда взялось. Поясню про последние два. Если приглядеться, то можно заметить что в уравнении присутствуют ещё и tg x, ctg x. А эти функции тоже не определены для всех x. Вспоминаем, что tg x = sinx/cos x, а ctg x = cos x / sin x. таким образом, эти две функции представляют собой дроби, а дробь определена, если знаменатель отличен от 0. Отсюда и следуют два последних условия.
2)Теперь просто решим уравнение, а потом учтём указанные выше ограничения. Это уравнение представляет собой показательно-тригонометрическое уравнение. И судя по основаниям(2 и 3) нам для начала неплохо бы привести все слагаемые к основанию 2 и 3, которые ещё не приведены. Сделаем это:


Теперь видим одинаковый множитель в обоих частях уравнения. Велик сооблазн от него избавиться. Но не спешим. Ведь делить обе части уравнения имеем лишь в том случае, если он отличен от 0. Так и есть. Показательная функция никогда не принимает значения 0(она принимает лишь положительные значения). Значит, теперь можем смело разделить на него:

Напомню, что всюду я пользовался свойствами степеней(думаю, они Вам известны).
Теперь пришли к совершенно элементарному показательному уравнению. Степени равны, основания степеней равны, значит, равны показатели.

Пришли к совершенно простому тригонометрическому уравнению. Учитывая, что ctg x = 1/tg x, вводим замену tg x = t
Получаем

Решаем его(это уравнение 8 класса):



Оба корня нам подходят(оба отличны от 0).
Корни ужасненькие получились, мягко говоря. Ну да ничего, не с таким сталкивались.
Дальше вспоминаем, что t = tg x. Решаем два полученных простейших уравнения и наконец-то находим x(дождались!).

Откуда всё это взялось, вопросов быть не должно в принципе к этому моменту, поэтому здесь я не останавливаюсь(просто добавлю, что n и k - целочисленные параметры).
на этом первую часть задачи(решение уравнения) можно считать законченной.
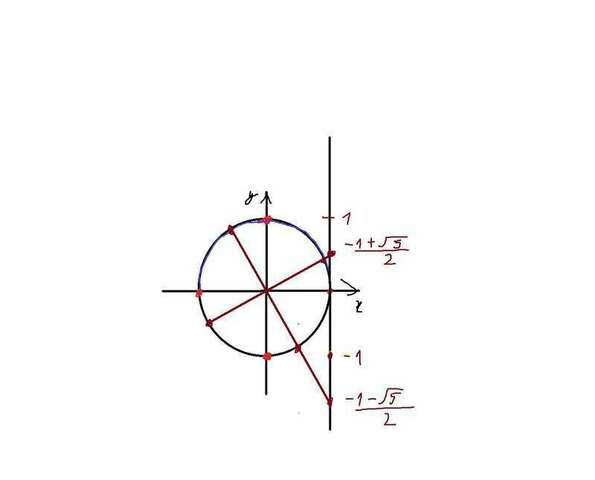
2)Приступим ко второй. Мы должны из найденных серий решений отбросить те, что нам не подходят по ограничениям. Сделаем это графически, конечно же. Именно, я нарисую картинку тригонометрического круга. Это "палочка-выручалочка" в сложных случаях наподобие нашего.
Я нарисовал круг. Потом красными точками отметил места, где синус и косинус равны 0. Затем отметил ось тангенсов, наметил на ней два наших значения тангенса(приближенно). Провёл через них прямые, соединяющие точки с центром окружности, они пересекли окружность в двух точках - это и есть серии решения нашего уравнения, просто в первый раз мы их записали формулой. Ещё у нас синус x должен быть положительным, это верхняя полуокружность, я её выделил синим цветом. Замечаем, что ни одна серия не даёт нулевого синуса или косинуса, поэтому возьмём лишь те точки, которые находятся в синей полуокружности.
Их две - это видно по рисунку. Осталось лишь дать им названия. В силу нехватки места я уже не останавливаюсь на этом. Просто скажу окончательный ответ:

Это и есть окончательный ответ.