Правильная 4-угольная пирамида имеет в основании квадрат.
Высота пирамиды h, половина диагонали d/2 основания и боковое ребро b образуют прям-ный тр-ник, в котором боковое ребро - это гипотенуза.
(d/2)^2 = b^2 - h^2
d = 2√(b^2 - h^2)
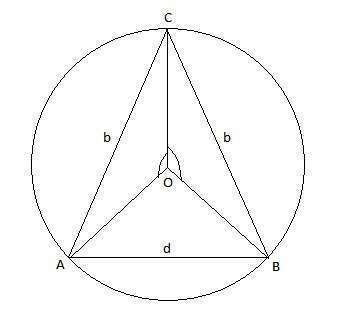
Теперь проведем сечение пирамиды через диагональ перпендикулярно к основанию. Получим равнобедренный тр-ник и описанную окружность.
Смотри рисунок.
У равнобедренного треугольника основание d и боковые стороны b.
Радиус описанной окружности можно найти из теоремы косинусов.
{ b^2 = R^2 + R^2 - 2*R*R*cos BOC = R^2*(2 - 2cos BOC)
{ d^2 = R^2 + R^2 - 2*R*R*cos AOB = R^2*(2 - 2cos AOB)
При этом углы AOC = BOC, AOB = 360 - 2*BOC
{ R^2 = b^2/(2 - 2cos BOC)
{ R^2 = d^2/(2 - 2cos AOB) = 4(b^2 - h^2)/(2 - 2cos(360 - 2*BOC))
Приравниваем правые части
b^2/(2 - 2cos BOC) = 2(b^2 - h^2)/(1 - cos (2*BOC))
cos (2*BOC) = 2cos^2 BOC - 1;
1 - cos (2*BOC) = 2 - 2cos^2 BOC
Здесь неизвестное - cos BOC, заменим его на x
Получаем из пропорции
b^2*(2 - 2x^2) = 2(b^2 - h^2)*(2 - 2x)
b^2*(1 - x^2) = 2(b^2 - h^2)*(1 - x)
b^2 - b^2*x^2 = 2b^2 - 2h^2 - 2(b^2 - h^2)*x
Получили квадратное уравнение
b^2*x^2 - 2(b^2 - h^2)*x + (b^2 - 2h^2) = 0
D/4 = (b^2 - h^2)^2 - b^2*(b^2 - 2h^2) =
= b^4 - 2b^2*h^2 + h^4 - b^4 + 2b^2*h^2 = h^4
x1 = (b^2 - h^2 - h^2)/b^2 = (b^2 - 2h^2)/b^2 = 1 - 2h^2/b^2
Это реальный корень
x2 = (b^2 - h^2 + h^2)/b^2 = b^2/b^2 = 1
Если x = cos BOC = 1, то BOC = 0, что невозможно.
Теперь подставляем найденный косинус в формулу радиуса
R^2 = b^2/(2 - 2cos BOC) = b^2/(2 - 2*(1 - 2h^2/b^2)) =
= b^2/(2 - 2 + 4h^2/b^2) = b^2/(4h^2/b^2) = b^4/(4h^2)
R = b^2/(2h)
Вот такая простая формула получилась из таких сложных уравнений.