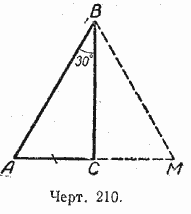
Теорема. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
Пусть в прямоугольном треугольнике АСВ угол В равен 30° (черт. 210). Тогда другой его острый угол будет равен 60°.
Докажем, что катет АС равен половине гипотенузы АВ. Продолжим катет АС за вершину прямого угла С и отложим отрезок СМ, равный отрезку АС. Точку М соединим с точкой В. Полученный треугольник ВСМ равен треугольнику АСВ. Мы видим, что каждый угол треугольника АВМ равен 60°, следовательно, этот треугольник — равносторонний.
Катет АС равен половине АМ, а так как АМ равняется АВ, то катет АС будет равен половине гипотенузы АВ.