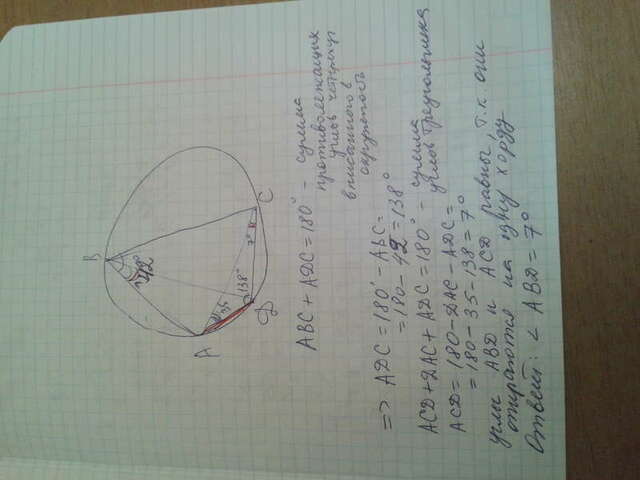
Угол ABC+ угол ADC=180 градусов
( так сумма противоположных углов вписанного в окружность четырехугольника равна 180 градусам)
ADC=180-ABC=180-42=38 (градусов)
ACD+DAC+ADC=180 (градусов) ( сумма углов треугольника равна 180 градусов)
ACD=180-DAC-ADC=180-35-138=7 (градусов)
углы ABD И ACD равны, так как опираются на одну хорду AD
значит ABD=ACD=7 ( градусов)
ответ 7 градусов
смотри решение в приложении( извини за неаккуратный рисунок)