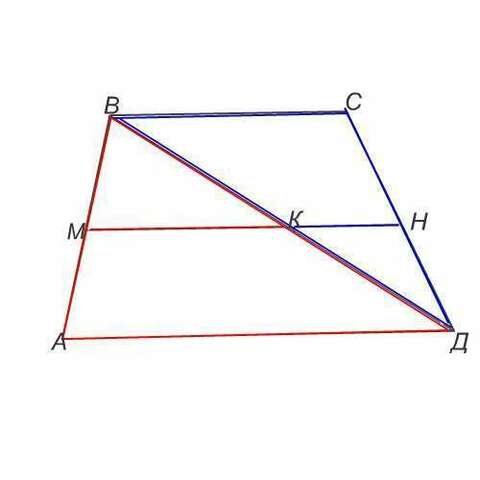
Диагональ делит трапецию на два треугольника: ᐃ АВД и ᐃ ВСД
В этих треугольниках основания - основания трапеции, а часть средней линии трапеции является средней линией каждого из треугольников соответственно.
Так как средняя линия трапеции делится диагональю на отрезки с разностью 2 см, а каждый из них является средней линией треугольников, найдем эти отрезки.
Пусть меньший отрезок ( средняя линия треугольника с меньшим основанием ВС) будет х
Тогда второй - х+2
х+2+х=10 см ( такова длина средней линии)
2х=8
х=4 см - длина меньшего отрезка. Он равен половине основания ВС
ВС=4*2=8 см
4+2=6 см - длина большего отрезка, он равен половине АД
АД=6*2=12 см