9(3) Отрезок MN параллелен основаниям трапеции АВСD, ВС=3, MN=5, ad=9. Чему равно отношение CN:ND?
------
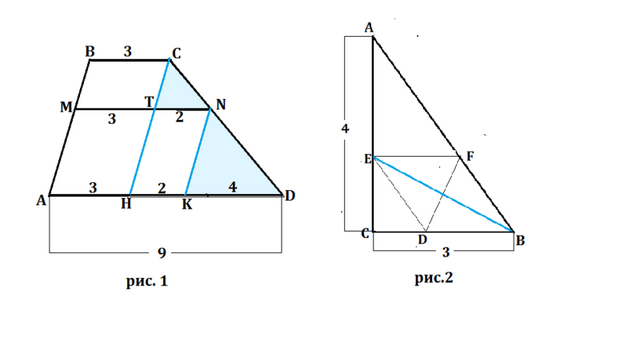
См. рис. 1 приложения.
Проведем из С отрезок СН параллельно ВА.
Точку пересечения с MN обозначим Т.
МN || AD, следовательно. МТ || АН и четырехугольники АМТН и МВСТ - параллелограммы.
МТ=АН=3. Тогда ТN=MN-MT=5-3=2
Из N проведем отрезок параллельно СН до пересечения с НD в точке К.
НК=TN=2,
КD=AD-AH-HK=4
В треугольниках NTC и DKN стороны СТ|| NK, TN|| KD, стороны СN и ND принадлежат стороне CD, следовательно, их углы равны. и
треугольники NTC и DKN подобны.
Отношения соответственных сторон подобных фигур равны.
СN:ND=TN:KD=2:4 или
1/2
----------
1(4)
Дан прямоугольный треугольник АВС с катетами ВС=3 и АС=3. Ромб BDEF расположен в треугольнике АВС, вершина В общая, а остальные три вершины ромба лежат на трех сторонах треугольника АВС.
Найти стороны ромба.
--
См. рис.2 приложения.
Угол В - угол ромба.
Диагонали ромба являются биссектрисами его углов.
Проведем биссектрису угла В до пересечения с АС в точке Е. ВЕ - диагональ ромба.
Стороны ромба параллельны.
Проведя EF||СB и ED || АВ получим рoмб BDEF
Биссектриса угла треугольника делит противоположную сторону в отношении прилежащих сторон.
АЕ:АЕ=АВ:ВС
АВ=5 ( треугольник АВС - египетский, можно проверить по т. Пифагора)
след., АЕ:ЕС=5:3
Треугольники АВС и АЕF подобны ( прямоугольные с общим острым углом при А).
АС:АЕ=ВС:EF
Пусть отношение отрезков стороны АС будет а.
Тогда АЕ=5а, ЕС=3а, АС=(5а+3а)=8а
8а:5а=3:EF
8 EF=15
EF=15/8=1 и 7/8 или 1,875