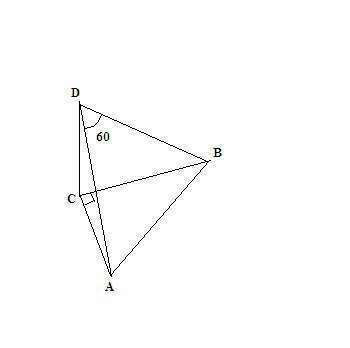
Это будет выглядеть примерно, как на рисунке.
Угол ACB = 90, ADB = 60, сторона AD = BD.
Треугольник ADB - равнобедренный с углом 60, т.е. равносторонний.
AD = BD = AB
Отрезок CD перпендикулярен к плоскости ABC.
Так как стороны AD = BD, и углы ADC = BDC, то проекции AC = BC.
Значит, треугольник ABC - прямоугольный и равнобедренный.
AC = BC = AB/√2 = AB*√2/2.
Но AD = AB.
В прямоугольном треугольнике ACD гипотенуза AD = AB,
а катет AC = AB*√2/2.
Значит, CD = AC = AB*√2/2 = AD*√2/2
Значит, треугольник ACD - тоже прямоугольный и равнобедренный.
Как и треугольник BCD.
Угол в прямоугольном равнобедренном треугольнике
ADC = CAD = 45 градусов.