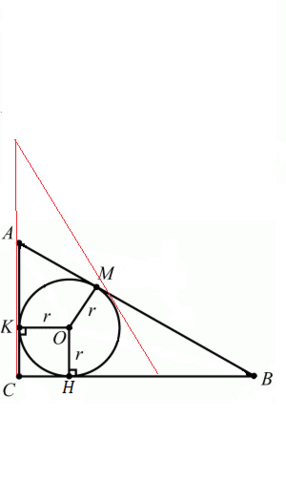
Т.к.
окружность вписанная, то АК=АМ и ВН=ВМ. Примем АК = Х, а ВМ = У. Тогда Х+У=26.
Отсюда У=26-Х. По теореме Пифагора АС²+ВС²
= АВ². Но АС = АК+КС = Х+r = X+4. ВС= ВН+СН = У+r = У+4. Тогда имеем
(Х+4)²+(Y+4)²=26². Раскроем
скобки Х²+8Х+16+У²+8У+16=26². Но У=26-Х. Тогда имеем Х²+8Х+16 +(26-Х)²+8(26-X)+16=26². Раскроем
скобки Х²+8Х+16+26²-52Х+Х²+8*26-8Х=26². Приведя общие члены и сократив что можно окончательно получим Х²-26Х+120=0. Решая это уравнение найдем Х1=20; Х2=6, Тогда У1=6; У2=20. Два решения потому, что возможен второй треугольник, такой же как и первый, но ориентирован иначе. (См. рисунок)
Таким образом АС = 6+4=10; ВС=20+4=24. Проверим верно ли найдены стороны. Должно выполнится уравнение 10²+24²=26²; 100+576 = 676. Равенство верное. Значит стороны найдены верно. Периметр = 10+24+26=60 см.