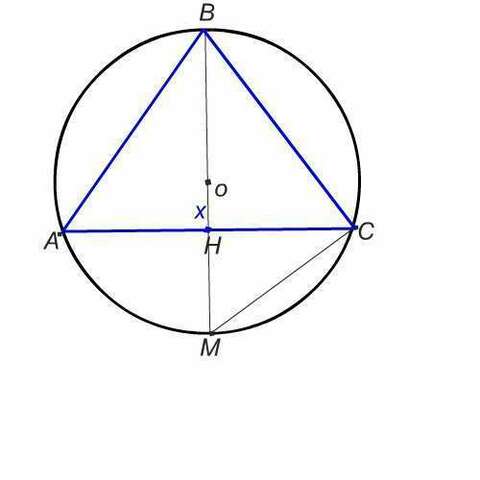
Рассмотрим рисунок, вложенный в решение.
ᐃ АВС - осевое сечение конуса, вписанного в шар с центром О.
АВ=ВС - его образующие
АС= диаметр основания конуса
НС- радиус основания конуса
ВН -высота конуса
ВМ- диаметр шара
ВО - радиус шара
Формула объема конуса
V=⅓ πr²h
Для нахождения объёма необходимо знать высоту ВН и радиус r конуса.
Высота ВН равна разности ВМ и МН
Соединим точку М диаметра шара и точку С диаметра конуса.
Рассмотрим треугольник ВСМ.
∠ВСМ - прямой, поскольку опирается на диаметр окружности.
Гипотенуза этого треугольника равна 2R и равна 10 см
Катет ВС - образующая конуса и равен 8 см
Катет МС по теореме Пифагора
МС =√(100-64)=6 см
Чтобы найти r, обозначим отрезок ОН = х.
Тогда
r=НС
ВН= 5+х
МН=5-х
Выразим высоту НС²= r² через известные величины треугольника ВСМ
r²=ВС² - ВН²
r²=МС²-МН²
Приравняем выражения, обозначающие значение r² (иначе НС²)
ВС² - ВН²=МС²-МН²
8² -(5+х)²= 6²-(5-х)²
64 - 25 -10х -х²=36 -25 +10х -х²
64 -10х =36 +10 х
28=20х
х=1,4
ОН=1,4
Из треугольника МНС найдем НС- радиус основания конуса
r²=МС²- МН²
МН=R - ОН=5-1,4 = 3,6 см
r²=36 -12,96=23,04
r=√23,04=4,8 см
V конуса=⅓ πr²h
V=π*4,8²*6,4:3=π*49,152 см³
или приближенно 154,4 см³ ( если на калькуляторе умножать на значение π )
-----
Вариант решения:
Для нахождения объёма необходимо знать высоту ВН и радиус r конуса.
Рассмотрим треугольник ВСМ.∠ВСМ - прямой, поскольку опирается на диаметр окружности.
Гипотенуза этого треугольника равна 2R и равна 10 см
Катет ВС - образующая конуса и равен 8 см
В прямоугольном треугольнике катет есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой. Иными словами, квадрат катета равен произведению всей гипотенузы на проекцию этого катета на гипотенузу.
В треугольнике ВСМ отрезок ВН - проекция катета ВС на гипотенузу. ВС²=ВН*ВМ
64=10*ВН
ВН=6,4 - это высота конуса.
СН - радиус конуса, который в то же время является высотой прямоугольного треугольника МВС, проведенной к гипотенузе.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой;
ВН мы нашли, он равен 6,4.
Отрезок НМ равен 10-6,4=3,6
СН²=6,4*3,6=23,04
СН=r=4,8
V конуса=⅓ πr²h
V=π*4,8²*6,4:3=π*49,152 см³