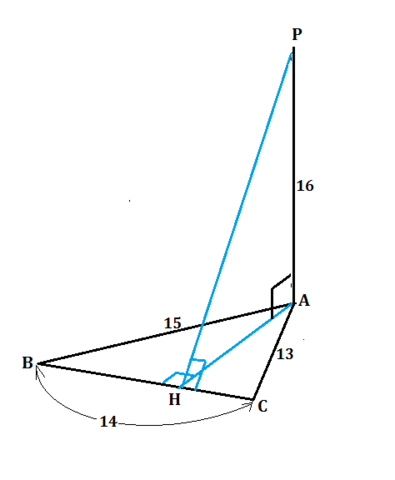
В треугольнике АВС сторона АВ=15 см, АС=13 см, СВ=14 см. Из вершины А восстановлен к его плоскости перпендикуляр, равный 16 см. Найдите расстояние от его концов до стороны ВС.
----
Расстояние от точки до прямой измеряется длиной перпендикулярного к ней отрезка.
Нужно
найти АН и
РН, перпендикулярные ВС.
АН - высота треугольника АВС.
Её можно найти из площади этого треугольника, вычисленной по т. Герона. Вычисления приводить не буду, сделать их самостоятельно несложно, а площадь этого треугольника равна
84.
Формула площади треугольника:
S=a*h:2
h=2S:a
АН=h
АН=168:14=
12 см
РН - перпендикулярно ВС по т. о трех перпендикулярах.
РН=√(АР²+АН²)=20 см