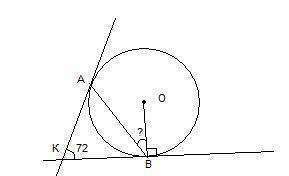
Используем свойство касательных, проведенных из одной точки: отрезки касательных к окружности (в нашем случае это КА и КВ), проведенные из одной точки (это К), равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности). Нам важно, что КА=КВ.
Треугольник АКВ получается таким образом равнобедренным, и углы при его основании АВ должны быть равными. Найдем их:
Угол КВО прямой, т.к. касательная к окружности КВ перпендикулярна к радиусу ОВ, проведенному в точку касания В. Отсюда
°