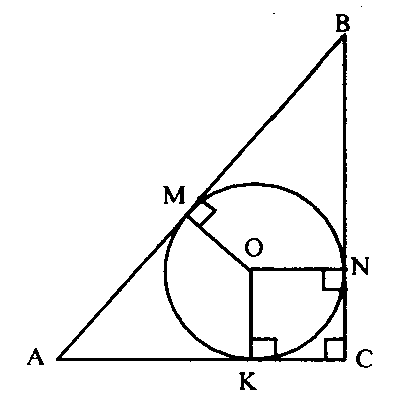
Pabc=(AM+AK)+(KC+CN)+(BM+BN)=2AM+2KC+2BM=2(AM+BM)+2KC=2(2R)+2r=4R+2r=2D+d.
пояснения:
AM=AK, KC=CN, BM=BN как отрезки касательных, проведенных из одной точки. AM+BM=2R - потому что центр описанной около треугольника окружности лежит на середине гипотенузы.
P.S. R и D- радиус и диаметр описанной окружности, r и d - вписанной.