Сначала упростим:
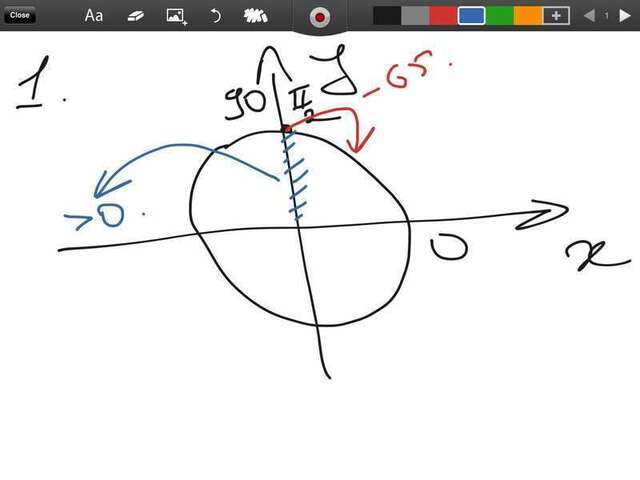
Возьмем, например, sin25 и представим его в таком виде:
sin25 = sin(90-65) = cos65
Над чертой Ox => sin > 0, значит остается + в измененной функции, 90 = pi/2 функция меняется на противоположную (возможно во вложениях будет понятнее)
единицу пока оставляем, упрощаем дальше то, что получилось, то есть:

В числителе получилась формула двойного угла, вот эта: sin2x = 2sinx*cosx
4sin65*cos65 = 2*(2sin65*cos65) = 2*sin2*65 = 2*sin130
Упрощаем дальше то, что получилось:

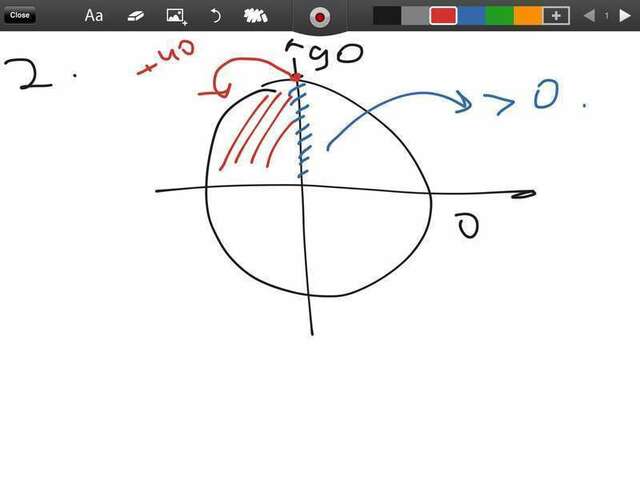
Теперь берем угол 130
sin130 = sin(90+40) = cos40
Упрощаем дальше:

и + 1, которую оставили сначала:
2+1 = 3.