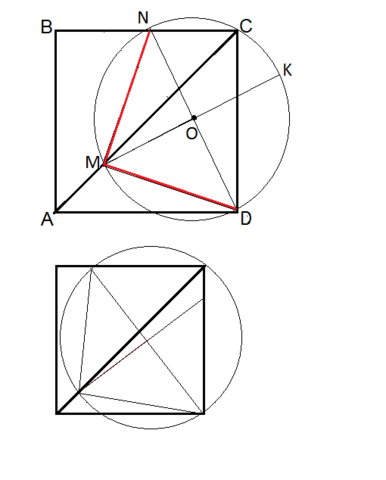
По условию MN=MD, следовательно, треугольник MND равнобедренный, и его высота МО является срединным перпендикуляром и его медианой. Если описать вокруг треугольника MND окружность, то, поскольку центр описанной окружности лежит на срединном перпендикуляре, диаметр МК пересечет DN по его середине в точке О.
Отрезок ND - гипотенуза прямоугольного треугольника DNC, D и N лежат на окружности. О - середина гипотенузы, ⇒ ON - радиус описанной вокруг треугольников NCD и MND , а ND- диаметр этой описанной окружности. Вписанный угол DMN опирается на диаметр и равен половине центрального угла MOD, т.е. угол DMN=180º:2=90º .
В равнобедренном прямоугольном треугольнике MDN сумма острых углов при основании ND равна 90º, эти углы равны и каждый из них равен 90º:2=45º. При этом их значение не будет зависеть от того, где выбрана точка М. Главное условие - равенство МN и MD.
Ответ: величина угла МДN=45º